Der Goldene Schnitt (φ)
Kunsthistoriker argumentieren, dass die Bedeutung des Goldenen Schnitts in der Kunstgeschichte übertrieben sein könnte
Der Goldene Schnitt verbindet Mathematik und Ästhetik und bleibt ein faszinierendes, wenn auch intuitives Werkzeug für Künstler*innen, um zeitlose Harmonie zu schaffen.
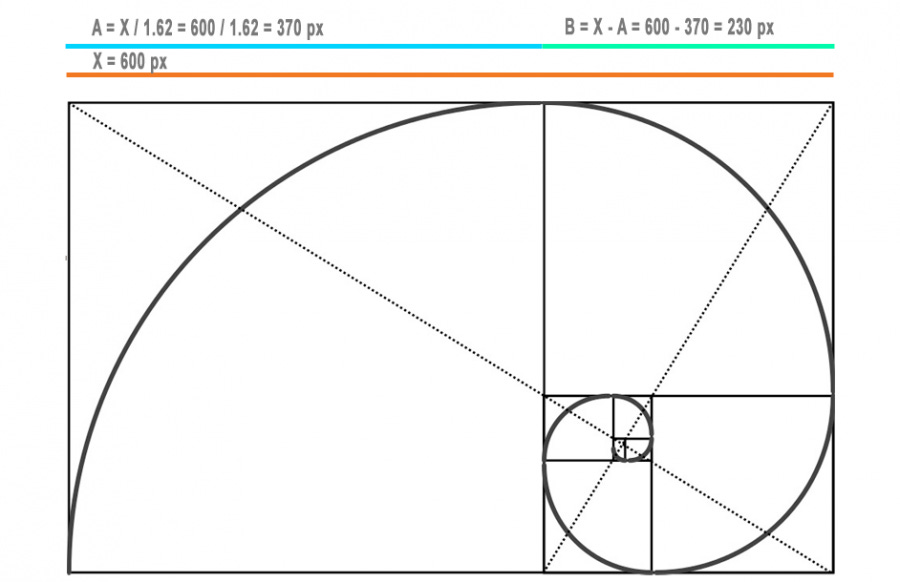
Die Formel des Goldenen Schnitt
Sie beschreibt das Teilungsverhältnis, das sowohl mathematisch als auch ästhetisch eine besondere Rolle spielt.
Die mathematische Herleitung und Bedeutung
Definition des Goldenen Schnitts
Der Goldene Schnitt liegt vor, wenn eine Strecke \(a + b\) so in zwei Teile \(a\) (länger) und \(b\) (kürzer) geteilt wird, dass das „Verhältnis der Gesamtstrecke zum längeren Teil“ gleich dem „Verhältnis des längeren zum kürzeren Teil“ ist.
Eigenschaften
Mit 5 die Quadratwurzel aus 5 bezeichnet.
Warum ist die Gleichung ästhetisch?
Das mathematische Prinzip des Goldenen Schnitts wird oft mit Harmonie assoziiert, da es in der Natur (Blütenblätter, Schneckenhäuser) und der Kunst als “intuitiv - angenehmes” Proportionenverhältnis wahrgenommen wird.
Unsicher ist, ob sich die Aufteilung des zweigeteilten Öffnen, wie es meinem Tor der Fall ist, eine logische Leitspur sein kann.
Das Triptychon beispielsweise funktionier in ähnlicher Weise und bezieht sich auf das altgriechische Wort “τρίπτυχος” tríptychos „in drei Teile gefaltet, aus drei Lagen bestehend“.
In Italien begann sich die Form des Triptychons im 15. Jahrhundert nach und nach aufzulösen, u. a. zugunsten der sogenannten Sacra Conversazione auf einer einzigen Bildtafel, wie schon in Fra Angelicos Annalena-Altar (kurz nach 1434)[2]. Andere Altäre zeigen zwar in der Unterteilung durch Bögen und bekrönende Giebel noch die Form eines Triptychons, sind jedoch als eine große Szene gestaltet, wie Lorenzo Monacos Marienkrönung (1414) und Anbetung der Könige (ca. 1421) in den Uffizien.
Künstler nutzen es also seit spätestens Mitte des 10. Jahrhunderts, um Kompositionen auszubalancieren (z. B. Bildformate, Platzierung von Objekten).
Beispiel
Ein Rechteck mit Seitenlängen im Verhältnis gilt als "goldenes Rechteck“. Teilt man es gemäß dem Goldenen Schnitt, entstehen unendlich viele kleinere goldene Rechtecke (Selbstähnlichkeit).
Die Formel ist keine willkürliche Zahl, sondern eine universelle mathematische Konstante, die strukturelle Harmonie beschreibt.
Obwohl ihre Bedeutung in der Kunst teils kritisch diskutiert wird, bleibt sie ein faszinierendes Bindeglied zwischen Mathematik, Natur und Ästhetik.
Beschreibung
Der Goldene Schnitt ist ein mathematisches Teilungsverhältnis, das in Kunst, Architektur und Natur als ästhetisch ideal gilt.
Er entsteht, wenn eine Strecke so geteilt wird, dass das Verhältnis des Ganzen zum größeren Teil dem Verhältnis des größeren zum kleineren Teils entspricht.
Dieses Prinzip wird oft mit Harmonie, Balance und Schönheit assoziiert.
Anwendung in der Kunst
Leonardo da Vinci nutzte den Goldenen Schnitt in Werken wie der „Mona Lisa“ und „Das Abendmahl“, um Komposition und Proportionen zu strukturieren.
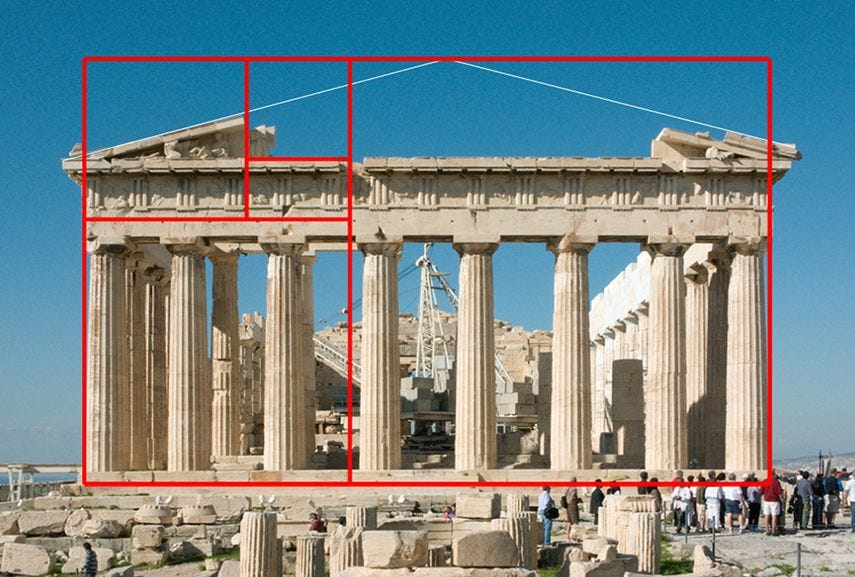
Die Parthenon-Fassade in Athen folgt dem Goldenen Schnitt, ebenso wie viele Renaissance-Gemälde und -Gebäude.
The-Parthenon-Finding-the-Golden-Section-everywhere
Moderne Künstler wie Salvador Dalí („Die Sakramente des letzten Abendmahls“) setzten ihn bewusst ein.
Salvador-Dali-Das-Sakrament-des-Letzten-Abendmahls-Nationale
Kontroverse
Einige Kunsthistoriker argumentieren, dass die Bedeutung des Goldenen Schnitts in der Kunstgeschichte übertrieben sein könnte. Dennoch bleibt er ein zentrales Konzept in ästhetischen Diskussionen.
KB
Quellen und Links
Triptychon
https://de.wikipedia.org/wiki/Triptychon
Encyclopædia Britannica
[Goldener Schnitt – Definition, Geschichte & Anwendung](https://www.britannica.com/science/golden-ratio)
Khan Academy
[Goldener Schnitt in Renaissance-Kunst](https://www.khanacademy.org/humanities/renaissance-reformation)
Livio, Mario (2002): The Golden Ratio - The Story of Phi, the World’s Most Astonishing Number
Wissenschaftliche Analyse historischer und kultureller Bezüge
- [Mona Lisa – Goldener Schnitt](https://commons.wikimedia.org/wiki/File:Mona_Lisa_Golden_Ratio.png)
- [Parthenon – Geometrische Analyse](https://commons.wikimedia.org/wiki/File:Parthenon_golden_ratio.svg)